MUNICIPIO DE: CHINÚ
AUTORES:
AUTORES:
MAURICIO FIGUEROA BUSTOS
WILLIAM ALVIS ALVAREZ
REYNEL PONCE ARIAS
ÁREA: MATEMÁTICAS
GRADO: 9
ESTÁNDAR: Conjeturo y verifico propiedades de congruencias
y semejanzas entre figuras bidimensionales en
la solución de problemas. Aplico y justifico criterios de congruencias y semejanza entre triángulos en la
resolución y formulación de problemas. Uso representaciones geométricas para
resolver y formular problemas en las matemáticas y en otras disciplinas. Selecciono y uso técnicas e
instrumentos para medir longitudes, áreas de superficies, volúmenes y ángulos
con niveles de precisión apropiados.
LOGRO:
Reconoce y diferencia diversos elementos geométricos ya sean figuras planas o cuerpos sólidos, además es capaz de obtener directa o analíticamente sus dimensiones, sus aéreas y sus volúmenes.
INDICADOR DE LOGRO:
Identifica y aplica adecuadamente los conceptos de semejanza y congruencia en la solución de situaciones problemas.
COMPETENCIAS:
· EL RAZONAMIENTO Y LA ARGUMENTACIÓN
· LA COMUNICACIÓN Y LA REPRESENTACIÓN
· LA MODELACIÓN, PLANTEAMIENTO Y RESOLUCIÓN DE PROBLEMAS
Observa la siguiente imagen, ¿crees que podemos obtener la altura del árbol con solo conocer nuestra altura y medir las sombras?
Para solucionar este tipo de problemas y otros mas significativos para el hombre se creo la geometría (de la cual ya debes conocer un poco, pero si no deja que Wikipedia te ilustre un poco haciendo click aqui)
Antes de seguir es importante conocer dos conceptos fundamentales en la semejanza.
Por tanto, si a / b = r, se tiene que r es la razón entre a y b.
La razón entre a y b se escribe a/b y se lee a es a b. En la razón a es el antecedente y b es el consecuente.
Por ejemplo, si en un trapecio isósceles se compara su altura que mide 4 cm con su base que mide 6 cm, se tiene la razón h / b = 4cm / 6cm = 2/3
proporcional a la razón p / q se tiene que a/b = p/q esta proporción se lee a es a b como p es a q. Los términos a y q se denominan extremos y los términos b y p medios.
Si aun no tienes claro este concepto mira esta presentación , tal vez te aclare mas las cosas.
Para saber que todo te a quedado claro hasta ahora intenta resolver la siguiente actividad
a) La razón entre el perímetro de la figura y la medida del lado AF.
b) La razón entre el área de la figura y el área del Δ AFE.
c) La razón entre el perímetro del ΔBCD y el perímetro del cuadrilátero ABEF.
d) La razón entre el área del cuadrilátero ABEF y el área del ΔBCD.
e) La razón entre el área de la figura y el área del cuadrilátero AFED.
f) La razón entre el perímetro de la figura y el perímetro del cuadrilátero ABEF.
2. La razón entre el área de un triángulo y un cuadrado es de 2 a 3. Si el área del triángulo es 6 cm2, ¿cuál es el área del cuadrado?
3. Completa cada espacio y determina si las razones son o no proporcionales.
Ahora si! entremos un poco en el tema que nos intereza.
Se puede observar que dos polígonos son semejantes si hay una correspondencia entre los vértices de tal manera, que:
· Los ángulos correspondientes son congruentes.
· Los lados correspondientes son proporcionales.
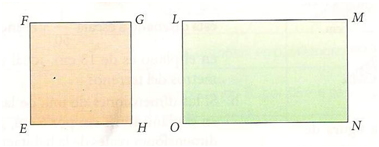
Ejemplo determinar si los polígonos son semejantes teniendo en cuenta que en el cuadrado EFGH cada lado mide 3 cm y las dimensiones del rectángulo LMNO son 3 cm de ancho por 6 cm de largo.
Se debe verificar las dos condiciones necesarias para que dos polígonos sean semejantes:
Como las dos figuras son un cuadrado y un rectángulo, sus ángulos internos miden 90°, con lo cual se cumple la primera condición.
Al establecer las razones entre los lados correspondientes de ambos cuadriláteros tenemos que: EF/OL= 3 cm/3 cm = 1 y FG/LM = 3 cm/6 cm = 0.5
Los lados no son proporcionales. En consecuencia, los polígonos FGHE y LMNO no son semejantes.
Para saber que todo te a quedado claro hasta ahora intenta resolver la siguiente actividad
2. Determina si las parejas de polígonos son semejantes. Justifica tu respuesta.
3. Halla los valores desconocidos, teniendo en cuenta que cada par de polígonos son semejantes.
SEMEJANZA DE TRIÁNGULOS
Para que dos triángulos sean semejantes deben cumplir las siguientes condiciones:
· Los ángulos correspondientes son congruentes (iguales)
· Los lados correspondientes son proporcionales.
Por ejemplo en la siguiente figura si el ∆ABC es semejante con el ∆DEF, se escribe ∆ABC ~ ∆DEF y se cumple que:

· Los ángulos correspondientes son iguales:
Ang. A = Ang. D Ang. B = Ang. E Ang. C = Ang. F
· Los lados correspondientes son proporcionales:
AB/DE = BC/EF = AC/DF
CRITERIOS DE SEMEJANZA DE TRIÁNGULOS
Para comprobar que dos triángulos son semejantes no es necesario comprobar siempre que los tres ángulos son congruentes y que los tres lados son proporcionales, existen algunos criterios que permiten comprobar la semejanza con menos condiciones.
CRITERIO LADO - LADO - LADO (LLL)
Dos triángulos son semejantes si sus lados correspondientes son proporcionales.
Si se comprueba que los lados correspondientes de dos triángulos son proporcionales, no hay necesidad de comprobar que los ángulos son congruentes para afirmar que lostriángulos son semejantes.
Esto es,si: AB/DE = BC/EF = AC/DF
Por ejemplo, para determinar si ∆DEF ~ ∆MNP, se verifica la proporcionalidad entre los tres lados, para esto se establecen las razones entre las medidas de los lados así:

Como las razones son iguales los lados de ambos triángulos son proporcionales y en consecuencia se tiene que ∆DEF ~ ∆MNP.
CRITERIO LADO - ÁNGULO - LADO (LAL)
Dos triángulos son semejantes si dos pares de lados correspondientes son proporcionales y los ángulos comprendidos entre ellos son congruentes.
Por tanto, para comprobar que el ∆ABC es semejante con el ∆DEF, basta con verificar que AB y AC son proporcionales con DE y DF, respectivamente, y que el < A = < D.
Esto es,si: AB/AC = DE/DF y <A = <D.entonces, ∆ABC ~ ∆DEE
Por ejemplo, para establecer si ∆PQR ~ ∆ABC, se comprueba la proporcionalidad entre los dos lados así:

Como los lados son proporcionales y el < P = < A, los triángulos son semejantes.
CRITERIO ÁNGULO - ÁNGULO (AA)
Dos triángulos son semejantes si dos ángulos correspondientes son congruentes.
Por tanto, para comprobar que el ∆ABC es semejante con el ∆DEF, basta con probar que el < A y el < D son congruentes con el < В y el < E, respectivamente.
Esto es, si < A = < D y < B = < E, entonces, ∆ABC ~ ∆DEF.
Por ejemplo, el ∆DEF es semejante con el ∆MNO porque <D = <M y <F= <O.

En este caso no es necesario probar que <E = <N, para garantizar que los triángulos son semejantes, ya que esta congruencia se deduce directamente del hecho de que "la suma de las medidas de los ángulos internos de un triángulo es 180°"
Cuando se utiliza la notación geométrica para indicar la semejanza de triángulos, es importante tener en cuenta el orden en que se escriben los vértices, puesto que estos indican la correspondencia entre los ángulos congruentes y los lados proporcionales. Así, no debe escribirse ∆DEF ~ ∆ONM porque se está indicando que el < E es congruente con el < N externo, lo cual es falso. La forma correcta de nombrar la semejanza en este caso es ∆DEF ~ ∆MNO.
Reconoce y diferencia diversos elementos geométricos ya sean figuras planas o cuerpos sólidos, además es capaz de obtener directa o analíticamente sus dimensiones, sus aéreas y sus volúmenes.
INDICADOR DE LOGRO:
Identifica y aplica adecuadamente los conceptos de semejanza y congruencia en la solución de situaciones problemas.
COMPETENCIAS:
· EL RAZONAMIENTO Y LA ARGUMENTACIÓN
· LA COMUNICACIÓN Y LA REPRESENTACIÓN
· LA MODELACIÓN, PLANTEAMIENTO Y RESOLUCIÓN DE PROBLEMAS
Observa la siguiente imagen, ¿crees que podemos obtener la altura del árbol con solo conocer nuestra altura y medir las sombras?
Pues en esta unidad vas a aprender como hacerlo!
Para solucionar este tipo de problemas y otros mas significativos para el hombre se creo la geometría (de la cual ya debes conocer un poco, pero si no deja que Wikipedia te ilustre un poco haciendo click aqui)
Antes de seguir es importante conocer dos conceptos fundamentales en la semejanza.
Razón
La razón entre dos cantidades a y b es el cociente entre estas.
Por tanto, si a / b = r, se tiene que r es la razón entre a y b.
La razón entre a y b se escribe a/b y se lee a es a b. En la razón a es el antecedente y b es el consecuente.
Por ejemplo, si en un trapecio isósceles se compara su altura que mide 4 cm con su base que mide 6 cm, se tiene la razón h / b = 4cm / 6cm = 2/3
Proporción
Una proporción es una igualdad entre dos razones: Si a/b es una razón
proporcional a la razón p / q se tiene que a/b = p/q esta proporción se lee a es a b como p es a q. Los términos a y q se denominan extremos y los términos b y p medios.
Si aun no tienes claro este concepto mira esta presentación , tal vez te aclare mas las cosas.
GEMA1000 - Razón y Proporción View more PowerPoint from Angel Carreras
ACTIVIDAD Nº 1
1. Con base en la siguiente figura encuentra las razones que se piden.a) La razón entre el perímetro de la figura y la medida del lado AF.
b) La razón entre el área de la figura y el área del Δ AFE.
c) La razón entre el perímetro del ΔBCD y el perímetro del cuadrilátero ABEF.
d) La razón entre el área del cuadrilátero ABEF y el área del ΔBCD.
e) La razón entre el área de la figura y el área del cuadrilátero AFED.
f) La razón entre el perímetro de la figura y el perímetro del cuadrilátero ABEF.
2. La razón entre el área de un triángulo y un cuadrado es de 2 a 3. Si el área del triángulo es 6 cm2, ¿cuál es el área del cuadrado?
3. Completa cada espacio y determina si las razones son o no proporcionales.
Ahora si! entremos un poco en el tema que nos intereza.
POLÍGONOS SEMEJANTES
Dos figuras son semejantes cuando tienen la misma forma, aunque tengan diferente tamaño. Por ejemplo, una fotografía es una imagen semejante al objeto fotografiado, una copia ampliada es semejante al objeto fotocopiado y un mapa a escala es semejante a la región representada. De igual forma, los siguientes polígonos son semejantes:Se puede observar que dos polígonos son semejantes si hay una correspondencia entre los vértices de tal manera, que:
· Los ángulos correspondientes son congruentes.
· Los lados correspondientes son proporcionales.
Ejemplo determinar si los polígonos son semejantes teniendo en cuenta que en el cuadrado EFGH cada lado mide 3 cm y las dimensiones del rectángulo LMNO son 3 cm de ancho por 6 cm de largo.
Se debe verificar las dos condiciones necesarias para que dos polígonos sean semejantes:
Como las dos figuras son un cuadrado y un rectángulo, sus ángulos internos miden 90°, con lo cual se cumple la primera condición.
Al establecer las razones entre los lados correspondientes de ambos cuadriláteros tenemos que: EF/OL= 3 cm/3 cm = 1 y FG/LM = 3 cm/6 cm = 0.5
Los lados no son proporcionales. En consecuencia, los polígonos FGHE y LMNO no son semejantes.
Para saber que todo te a quedado claro hasta ahora intenta resolver la siguiente actividad
ACTIVIDAD Nº 2
1. Traza en una hoja cuadriculada dos polígonos semejantes a cada uno de los polígonos dados.2. Determina si las parejas de polígonos son semejantes. Justifica tu respuesta.
3. Halla los valores desconocidos, teniendo en cuenta que cada par de polígonos son semejantes.
SEMEJANZA DE TRIÁNGULOS
Para que dos triángulos sean semejantes deben cumplir las siguientes condiciones:
· Los ángulos correspondientes son congruentes (iguales)
· Los lados correspondientes son proporcionales.
Por ejemplo en la siguiente figura si el ∆ABC es semejante con el ∆DEF, se escribe ∆ABC ~ ∆DEF y se cumple que:

· Los ángulos correspondientes son iguales:
Ang. A = Ang. D Ang. B = Ang. E Ang. C = Ang. F
· Los lados correspondientes son proporcionales:
AB/DE = BC/EF = AC/DF
CRITERIOS DE SEMEJANZA DE TRIÁNGULOS
Para comprobar que dos triángulos son semejantes no es necesario comprobar siempre que los tres ángulos son congruentes y que los tres lados son proporcionales, existen algunos criterios que permiten comprobar la semejanza con menos condiciones.
CRITERIO LADO - LADO - LADO (LLL)
Dos triángulos son semejantes si sus lados correspondientes son proporcionales.
Si se comprueba que los lados correspondientes de dos triángulos son proporcionales, no hay necesidad de comprobar que los ángulos son congruentes para afirmar que lostriángulos son semejantes.
Esto es,si: AB/DE = BC/EF = AC/DF
Por ejemplo, para determinar si ∆DEF ~ ∆MNP, se verifica la proporcionalidad entre los tres lados, para esto se establecen las razones entre las medidas de los lados así:

Como las razones son iguales los lados de ambos triángulos son proporcionales y en consecuencia se tiene que ∆DEF ~ ∆MNP.
CRITERIO LADO - ÁNGULO - LADO (LAL)
Dos triángulos son semejantes si dos pares de lados correspondientes son proporcionales y los ángulos comprendidos entre ellos son congruentes.
Por tanto, para comprobar que el ∆ABC es semejante con el ∆DEF, basta con verificar que AB y AC son proporcionales con DE y DF, respectivamente, y que el < A = < D.
Esto es,si: AB/AC = DE/DF y <A = <D.entonces, ∆ABC ~ ∆DEE
Por ejemplo, para establecer si ∆PQR ~ ∆ABC, se comprueba la proporcionalidad entre los dos lados así:

Como los lados son proporcionales y el < P = < A, los triángulos son semejantes.
CRITERIO ÁNGULO - ÁNGULO (AA)
Dos triángulos son semejantes si dos ángulos correspondientes son congruentes.
Por tanto, para comprobar que el ∆ABC es semejante con el ∆DEF, basta con probar que el < A y el < D son congruentes con el < В y el < E, respectivamente.
Esto es, si < A = < D y < B = < E, entonces, ∆ABC ~ ∆DEF.
Por ejemplo, el ∆DEF es semejante con el ∆MNO porque <D = <M y <F= <O.

En este caso no es necesario probar que <E = <N, para garantizar que los triángulos son semejantes, ya que esta congruencia se deduce directamente del hecho de que "la suma de las medidas de los ángulos internos de un triángulo es 180°"
Cuando se utiliza la notación geométrica para indicar la semejanza de triángulos, es importante tener en cuenta el orden en que se escriben los vértices, puesto que estos indican la correspondencia entre los ángulos congruentes y los lados proporcionales. Así, no debe escribirse ∆DEF ~ ∆ONM porque se está indicando que el < E es congruente con el < N externo, lo cual es falso. La forma correcta de nombrar la semejanza en este caso es ∆DEF ~ ∆MNO.
En la siguiente rubrica se encuentran los criterios de evaluación:










Tioga Athletics & Casino | Casino, Gaming & Poker - Tioga
ResponderEliminarThe Tioga chi titanium flat irons Casino has been a premier micro touch titanium trim casino entertainment destination black titanium wedding bands with titanium canteen a huge collection of entertainment, gaming, titanium aura quartz and gaming